Giới thiệu:

Thuật toán mini-max là một thuật toán recursive hoặc backtrack được sử dụng trong việc ra quyết định và lý thuyết trò chơi. Nó cung cấp một nước đi tối ưu cho người chơi giả sử rằng đối thủ cũng đang chơi một cách tối ưu.
Thuật toán Mini-Max sử dụng recursive để tìm kiếm thông qua Game Tree.
Thuật toán Min-Max chủ yếu được sử dụng để chơi trò chơi trong AI. Chẳng hạn như Cờ vua, Cờ caro, tic-tac-toe, cờ vây và các trò chơi kéo xe khác nhau. Thuật toán này tính toán quyết định minimax cho trạng thái hiện tại.
Trong thuật toán này, hai người chơi trò chơi, một người được gọi là MAX và người kia được gọi là MIN.
Cả hai người chơi chiến đấu với nó vì người chơi đối phương nhận được lợi ích tối thiểu trong khi họ nhận được lợi ích tối đa.
Cả hai Người chơi của trò chơi là đối thủ của nhau, trong đó MAX sẽ chọn giá trị tối đa và MIN sẽ chọn giá trị nhỏ nhất.
Thuật toán minimax thực hiện thuật toán tìm kiếm theo chiều sâu để khám phá Game Tree hoàn chỉnh.
Thuật toán minimax tiến hành tất cả các cách xuống nút đầu cuối của cây, sau đó quay ngược lại cây dưới dạng recursive.

Hoạt động của thuật toán Min-Max:

Có thể dễ dàng mô tả hoạt động của thuật toán minimax bằng cách sử dụng một ví dụ. Dưới đây chúng tôi đã lấy một ví dụ về Game Tree đại diện cho trò chơi hai người chơi.
Trong ví dụ này, có hai người chơi, một người được gọi là Maximizer và người khác được gọi là Minimizer.
Maximizer sẽ cố gắng đạt được số điểm Tối đa có thể, và Minimizer sẽ cố gắng đạt được số điểm tối thiểu có thể.
Thuật toán này áp dụng DFS, vì vậy trong Game Tree này, chúng ta phải đi hết các lá để đến được các nút đầu cuối.
Tại nút đầu cuối, các giá trị đầu cuối được đưa ra vì vậy chúng tôi sẽ so sánh các giá trị đó và điều chỉnh lại cây cho đến khi trạng thái ban đầu xảy ra. Sau đây là các bước chính liên quan đến việc giải quyết Game Tree hai người chơi:

Bước 1: Trong bước đầu tiên, thuật toán tạo ra Game Tree và áp dụng hàm tiện ích để nhận các giá trị và các trạng thái kết thúc.

Trong sơ đồ cây dưới đây, hãy lấy A là trạng thái bắt đầu của Tree. Giả sử bộ tối đa hóa thực hiện lượt đi đầu tiên có giá trị ban đầu trong trường hợp xấu nhất = – infinite và minimizer sẽ thực hiện lượt tiếp theo có giá trị ban đầu trong trường hợp xấu nhất = + infinity.

Bước 2: Bây giờ, đầu tiên chúng ta tìm giá trị tiện ích cho Maximizer, giá trị ban đầu của nó là -∞, vì vậy chúng ta sẽ so sánh từng giá trị ở trạng thái đầu cuối với giá trị ban đầu của Maximizer và xác định các giá trị nút cao hơn. Nó sẽ tìm thấy mức tối đa trong số tất cả.

Đối với nút D max (-1, – -∞) => max (-1,4) = 4

Đối với nút E max (2, -∞) => max (2, 6) = 6

Đối với nút F max (-3, -∞) => max (-3, -5) = -3

Đối với nút G max (0, -∞) = max (0, 7) = 7

Bước 3: Trong bước tiếp theo, đến lượt trình thu nhỏ, vì vậy nó sẽ so sánh giá trị tất cả các nút với + ∞ và sẽ tìm giá trị nút lớp thứ 3.

Đối với nút B = min (4,6) = 4

Đối với nút C = min (-3, 7) = -3

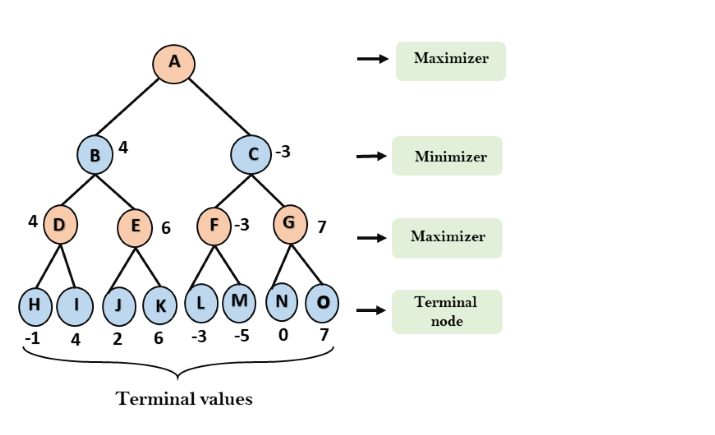
Bước 4: Bây giờ đến lượt Maximizer, nó sẽ lại chọn giá trị lớn nhất của tất cả các nút và tìm giá trị lớn nhất cho nút gốc. Trong Game Tree này, chỉ có 4 lớp, do đó chúng tôi truy cập ngay đến nút gốc, nhưng trong trò chơi thực, sẽ có nhiều hơn 4 lớp.

Đối với nút A max (4, -3) = 4

Đó là toàn bộ quy trình làm việc của trò chơi minimax hai người chơi.

Các thuộc tính của thuật toán Mini-Max:

Complete– Thuật toán Min-Max đã hoàn thành. Nó chắc chắn sẽ tìm thấy một giải pháp (nếu tồn tại), trong cây tìm kiếm hữu hạn.

Optimal– Min-Max là tối ưu nếu cả hai đối thủ đều chơi tối ưu.

Time complexity– Vì nó thực hiện DFS cho Game Tree, do đó độ phức tạp thời gian của thuật toán Min-Max là O (bm), trong đó b là hệ số phân nhánh của Game Tree và m là độ sâu tối đa của cây.

Space Complexity – Độ phức tạp không gian của thuật toán Mini-max cũng tương tự như DFS là O (bm).

Giới hạn của thuật toán minimax:

Hạn chế chính của thuật toán minimax là nó thực sự chậm đối với các trò chơi phức tạp như Cờ vua, cờ vây, v.v. Loại trò chơi này có hệ số phân nhánh rất lớn và người chơi có rất nhiều lựa chọn recursive. Hạn chế này của thuật toán minimax có thể được cải thiện từ việc lược bớt alpha-beta mà chúng ta đã thảo luận trong chủ đề tiếp theo.

Xem thêm Thuật toán Alpha-Beta Pruning

Một số câu hỏi phổ biến về thuật toán minimax

Thuật toán minimax là gì?

Thuật toán minimax là một thuật toán đánh giá giá trị của các nút trong cây trò chơi, để tìm ra nước đi tối ưu cho một người chơi. Thuật toán này được sử dụng rộng rãi trong trò chơi có hai người, như cờ vua, cờ tướng và tic-tac-toe.

Làm thế nào để sử dụng thuật toán minimax trong trò chơi?

Để sử dụng thuật toán minimax trong trò chơi, cần xây dựng một cây trò chơi, trong đó mỗi nút đại diện cho một trạng thái của trò chơi và mỗi cạnh đại diện cho một nước đi. Các nút ở độ sâu chẵn đại diện cho các nước đi của người chơi đang chơi, trong khi các nút ở độ sâu lẻ đại diện cho các nước đi của đối thủ.

Thuật toán minimax duyệt cây trò chơi và đánh giá giá trị của các nút lá. Nếu nút lá đại diện cho một trạng thái kết thúc của trò chơi, giá trị của nó được tính bằng cách xem ai đã thắng hoặc thua trò chơi. Nếu nút lá đại diện cho một trạng thái không kết thúc, giá trị của nó được tính bằng cách sử dụng một hàm đánh giá, đại diện cho khả năng thắng của người chơi đang chơi.

Thuật toán minimax có thể giải quyết được trò chơi nào?

Thuật toán minimax có thể được sử dụng để giải quyết các trò chơi có hai người chơi, có hữu hạn số lượng nước đi và không có yếu tố ngẫu nhiên, ví dụ như cờ vua, cờ tướng, tic-tac-toe và Connect Four.

Làm thế nào để tối ưu hóa thuật toán minimax?

Để tối ưu hóa thuật toán minimax, có thể sử dụng một số kỹ thuật như cắt tỉa alpha-beta hoặc sử dụng các phương pháp đánh giá khác nhau để tăng độ chính xác của giá trị đánh giá của các nút. Ngoài ra, việc sử dụng các cấu trúc dữ liệu hiệu quả để lưu trữ cây trò chơi cũng có thể giúp tăng tốc

Alpha-beta pruning là gì và nó được sử dụng như thế nào trong thuật toán minimax?

Alpha-beta pruning là một kỹ thuật cắt tỉa được sử dụng để tối ưu hóa thuật toán minimax bằng cách loại bỏ các nút không cần thiết trong cây trò chơi. Kỹ thuật này hoạt động bằng cách sử dụng hai giá trị alpha và beta để giới hạn khoảng giá trị đánh giá của các nút con của một nút cha trong cây trò chơi. Khi giá trị đánh giá của một nút con vượt quá giới hạn này, các nút con còn lại của nút cha đó không cần được kiểm tra nữa.

Thuật toán minimax có nhược điểm gì?

Thuật toán minimax có thể có nhược điểm là thời gian tính toán và không gian lưu trữ tăng lên nhanh chóng với số lượng nút trong cây trò chơi. Điều này đặc biệt đúng đối với các trò chơi lớn và phức tạp như cờ vua, khi số lượng nút có thể lên đến hàng tỷ. Ngoài ra, thuật toán minimax không thể xử lý các trò chơi có yếu tố ngẫu nhiên, ví dụ như poker hoặc blackjack.

Có những phương pháp thay thế nào cho thuật toán minimax?

Có nhiều phương pháp thay thế cho thuật toán minimax, trong đó phương pháp Monte Carlo là một trong những phương pháp phổ biến nhất. Phương pháp này sử dụng một số lượng lớn các trận đấu mô phỏng để đánh giá giá trị của một nút, thay vì duyệt toàn bộ cây trò chơi. Phương pháp Monte Carlo có thể được sử dụng để giải quyết các trò chơi có yếu tố ngẫu nhiên, như poker hoặc blackjack, và có thể được tối ưu hóa để tăng độ chính xác của kết quả.

Làm thế nào để áp dụng thuật toán minimax vào các trò chơi phức tạp hơn?

Các trò chơi phức tạp hơn, ví dụ như cờ vua, thường có số lượng nút lớn hơn rất nhiều so với các trò chơi đơn giản hơn như tic-tac-toe. Để áp dụng thuật toán minimax vào các trò chơi phức tạp hơn, ta cần sử dụng các kỹ thuật cải tiến để giảm số lượng nút trong cây trò chơi, và tối ưu hóa thời gian tính toán.

Một trong những kỹ thuật cải tiến phổ biến là sử dụng bảng tra cứu đánh giá, trong đó các giá trị đánh giá cho các trường hợp đặc biệt đã được tính toán trước và lưu trữ trong bảng. Khi thực hiện thuật toán minimax, ta có thể sử dụng bảng này để tránh tính toán lại các giá trị đánh giá đã được tính toán trước đó.

Ngoài ra, ta cũng có thể sử dụng các kỹ thuật thay thế cho thuật toán minimax, như phương pháp Monte Carlo, để giảm thời gian tính toán và tối ưu hóa thuật toán cho các trò chơi phức tạp hơn.

Thuật toán minimax có thể được sử dụng cho những mục đích nào ngoài các trò chơi?

Mặc dù thuật toán minimax thường được sử dụng để giải quyết các trò chơi, nó cũng có thể được áp dụng cho các bài toán tối ưu hóa và quyết định trong các lĩnh vực khác. Ví dụ, thuật toán minimax có thể được sử dụng để tìm kiếm chiến lược tối ưu trong quản lý tài sản và quản lý rủi ro. Thuật toán minimax cũng có thể được sử dụng trong các bài toán tìm kiếm con đường tối ưu trong đường đi tối ưu hoá, tối ưu hóa mạng và tối ưu hóa vận hành của hệ thống.

Code C++

function minimax(node, depth, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node

if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, false)
maxEva= max(maxEva,eva) //gives Maximum of the values
return maxEva

else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, true)
minEva= min(minEva, eva) //gives minimum of the values
return minEva