Giới thiệu

Alpha-Beta Pruning là một phiên bản sửa đổi của thuật toán minimax. Nó là một kỹ thuật tối ưu hóa cho thuật toán minimax.

Như chúng ta đã thấy trong thuật toán tìm kiếm minimax rằng số lượng trạng thái trò chơi mà nó phải kiểm tra là cấp số nhân theo chiều sâu của cây. Vì chúng ta không thể loại bỏ số mũ, nhưng chúng ta có thể cắt nó thành một nửa. Do đó, có một kỹ thuật mà không cần kiểm tra từng nút của cây trò chơi, chúng ta có thể tính ra quyết định minimax chính xác và kỹ thuật này được gọi là cắt tỉa. Điều này liên quan đến hai tham số ngưỡng Alpha và beta để mở rộng trong tương lai, vì vậy nó được gọi là Alpha-Beta Pruning. Nó còn được gọi là Thuật toán Alpha-Beta.

Thuật toán Alpha-Beta Pruning

Alpha – beta pruning là một thuật toán tìm kiếm nâng cao của minimax, thuật toán này làm giảm số lượng các node cây được đánh giá bởi thuật toán minimax trong cây tìm kiếm. Thuật toán này dựa theo tìm kiếm đối nghịch trong một số trò chơi với máy (Tic-tac-toe, Cờ vua, v.v.).

Alpha-Beta Pruning có thể được áp dụng ở bất kỳ độ sâu nào của cây, và đôi khi nó không chỉ cắt tỉa lá cây mà còn cắt tỉa toàn bộ cây phụ.

Hai tham số có thể được định nghĩa là:

Alpha: Sự lựa chọn tốt nhất (giá trị cao nhất) mà chúng tôi đã tìm thấy cho đến nay tại bất kỳ điểm nào trên con đường của Maximizer. Giá trị ban đầu của alpha là -∞.
Beta: Lựa chọn tốt nhất (giá trị thấp nhất) mà chúng tôi đã tìm thấy cho đến nay tại bất kỳ điểm nào dọc theo đường dẫn của Minimizer. Giá trị ban đầu của beta là + ∞.

Việc Alpha-Beta Pruning thành một thuật toán minimax tiêu chuẩn trả lại cùng một động thái như thuật toán tiêu chuẩn, nhưng nó loại bỏ tất cả các nút không thực sự ảnh hưởng đến quyết định cuối cùng nhưng làm cho thuật toán bị chậm. Do đó, bằng cách lược bỏ các nút này, thuật toán sẽ nhanh hơn.

Lưu ý: Để hiểu rõ hơn về chủ đề này, vui lòng nghiên cứu thuật toán minimax.

Điều kiện để Alpha-Beta Pruning:

Điều kiện chính cần thiết để Alpha-Beta Pruning là:

α> = β

Những điểm chính về việc Alpha-Beta Pruning:

Max player sẽ chỉ cập nhật giá trị của alpha.
Min player sẽ chỉ cập nhật giá trị của phiên bản beta.
Trong khi backtracking lại cây, các giá trị của nút sẽ được chuyển đến các nút phía trên thay vì các giá trị của alpha và beta.
Chúng tôi sẽ chỉ chuyển các giá trị alpha, beta cho các nút con.

Làm việc của Alpha-Beta Pruning:

Hãy lấy một ví dụ về cây tìm kiếm hai người chơi để hiểu hoạt động của việc Alpha-Beta Pruning

Bước 1: Ở bước đầu tiên, người chơi Max sẽ bắt đầu di chuyển đầu tiên từ nút A nơi α = -∞ và β = + ∞, những giá trị alpha và beta này được truyền lại cho nút B nơi lại α = -∞ và β = + ∞ và Nút B chuyển cùng một giá trị cho nút con D của nó.

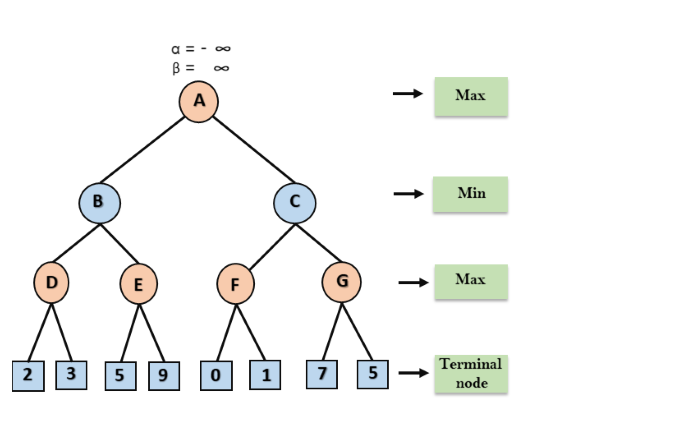
Bước 2: Tại nút D, giá trị của α sẽ được tính theo lượt của nó cho Max. Giá trị của α được so sánh với đầu tiên là 2 và sau đó là 3, và max (2, 3) = 3 sẽ là giá trị của α tại nút D và giá trị của nút cũng sẽ là 3.

Bước 3: Bây giờ thuật toán quay ngược lại nút B, trong đó giá trị của β sẽ thay đổi vì đây là lượt của Min, Bây giờ β = + ∞, sẽ so sánh với giá trị của các nút tiếp theo có sẵn, tức là min (∞, 3) = 3, do đó tại nút B bây giờ α = -∞ và β = 3.

Trong bước tiếp theo, thuật toán duyệt qua nút kế tiếp tiếp theo của nút B là nút E, và các giá trị của α = -∞ và β = 3 cũng sẽ được chuyển.

Bước 4: Tại nút E, Max sẽ đến lượt, và giá trị của alpha sẽ thay đổi. Giá trị hiện tại của alpha sẽ được so sánh với 5, vì vậy max (-∞, 5) = 5, do đó tại nút E α = 5 và β = 3, trong đó α> = β, vì vậy kế thừa bên phải của E sẽ bị lược bỏ, và thuật toán sẽ không đi qua nó, và giá trị tại nút E sẽ là 5.

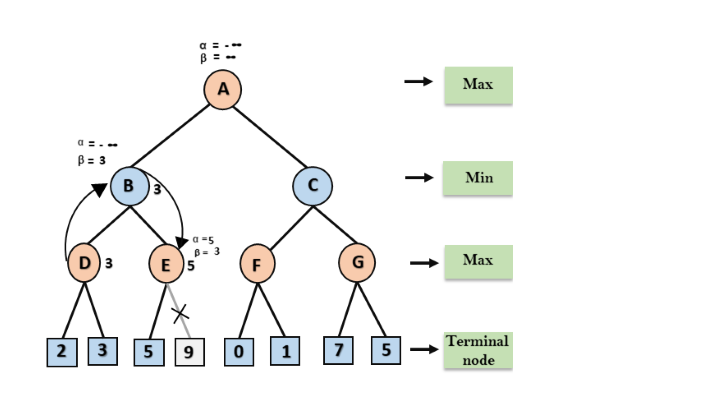
Bước 5: Ở bước tiếp theo, thuật toán lại chiếu ngược cây, từ nút B đến nút A. Tại nút A, giá trị của alpha sẽ được thay đổi giá trị lớn nhất có sẵn là 3 như max (-∞, 3) = 3 và β = + ∞, hai giá trị này bây giờ được chuyển đến người kế nhiệm bên phải của A là Nút C.

Tại nút C, α = 3 và β = + ∞, và các giá trị tương tự sẽ được chuyển cho nút F.

Bước 6: Tại nút F, một lần nữa giá trị của α sẽ được so sánh với nút con bên trái là 0 và max (3,0) = 3, sau đó so sánh với nút con bên phải là 1 và max (3,1) = 3 vẫn còn α vẫn là 3, nhưng giá trị nút của F sẽ trở thành 1.

Bước 7: Nút F trả về giá trị nút 1 cho nút C, tại C α = 3 và β = + ∞, ở đây giá trị beta sẽ được thay đổi, nó sẽ so sánh với 1 nên min (∞, 1) = 1. Bây giờ tại C, α = 3 và β = 1, và một lần nữa nó thỏa mãn điều kiện α> = β, vì vậy con tiếp theo của C là G sẽ bị lược bớt, và thuật toán sẽ không tính toàn bộ cây con G.

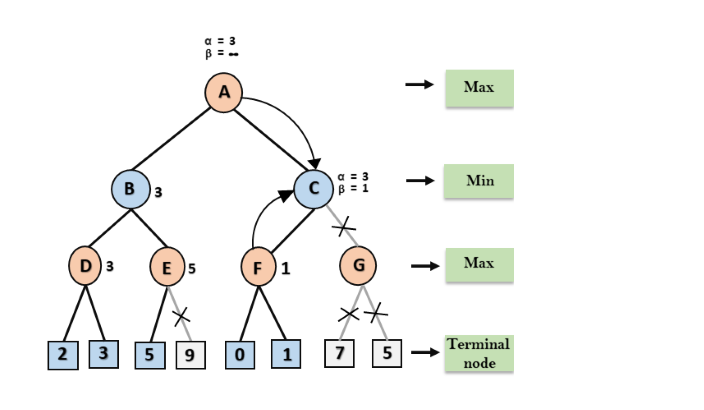
Bước 8: C bây giờ trả về giá trị từ 1 đến A ở đây giá trị tốt nhất cho A là max (3, 1) = 3. Sau đây là cây trò chơi cuối cùng là hiển thị các nút được tính toán và các nút chưa bao giờ tính toán. Do đó, giá trị tối ưu cho bộ cực đại là 3 cho ví dụ này.

Di chuyển thứ tự trong Alpha-Beta Pruning:

Hiệu quả của việc Alpha-Beta Pruning phụ thuộc nhiều vào thứ tự mà mỗi nút được kiểm tra. Thứ tự di chuyển là một khía cạnh quan trọng của việc Alpha-Beta Pruning.

Nó có thể có hai loại:

Worst ordering: Trong một số trường hợp, thuật toán Alpha-Beta Pruning không cắt tỉa bất kỳ lá nào của cây và hoạt động chính xác như thuật toán minimax. Trong trường hợp này, nó cũng tiêu tốn nhiều thời gian hơn vì các yếu tố alpha-beta, động thái cắt tỉa như vậy được gọi là thứ tự tồi tệ nhất. Trong trường hợp này, chuyển động tốt nhất xảy ra ở phía bên phải của cây. Độ phức tạp về thời gian cho một lệnh như vậy là O (bm).

Ideal ordering: Thứ tự lý tưởng để Alpha-Beta Pruning xảy ra khi nhiều lần cắt tỉa diễn ra trên cây và các động thái tốt nhất xảy ra ở phía bên trái của cây. Chúng tôi áp dụng DFS do đó nó tìm kiếm đầu tiên bên trái của cây và đi sâu gấp đôi so với thuật toán minimax trong cùng một khoảng thời gian. Độ phức tạp trong thứ tự lý tưởng là O (bm / 2).

Các quy tắc để tìm thứ tự tốt:

Sau đây là một số quy tắc để tìm thứ tự tốt trong việc Alpha-Beta Pruning:

Xảy ra nước đi tốt nhất từ nút nông nhất.
Thứ tự các nút trong cây sao cho các nút tốt nhất được kiểm tra trước.
Sử dụng kiến thức miền trong khi tìm ra nước đi tốt nhất. Ví dụ: đối với Cờ vua, hãy thử thứ tự: bắt trước, sau đó đe dọa, sau đó tiến lên, lùi lại.
Chúng tôi có thể ghi sổ các trạng thái, vì có khả năng các trạng thái đó có thể lặp lại.

Code:

function minimax(node, depth, alpha, beta, maximizingPlayer) is
if depth ==0 or node is a terminal node then
return static evaluation of node

if MaximizingPlayer then // for Maximizer Player
maxEva= -infinity
for each child of node do
eva= minimax(child, depth-1, alpha, beta, False)
maxEva= max(maxEva, eva)
alpha= max(alpha, maxEva)
if beta<=alpha
break
return maxEva

else // for Minimizer player
minEva= +infinity
for each child of node do
eva= minimax(child, depth-1, alpha, beta, true)
minEva= min(minEva, eva)
beta= min(beta, eva)
if beta<=alpha
break
return minEva