Decision Tree là gì?

Nó là một công cụ có các ứng dụng bao gồm nhiều lĩnh vực khác nhau. Decision Tree có thể được sử dụng để phân loại cũng như các bài toán hồi quy. Bản thân cái tên gợi ý rằng nó sử dụng một sơ đồ giống như cấu trúc cây để hiển thị các dự đoán là kết quả của một loạt các phân tách dựa trên tính năng. Nó bắt đầu với một Root Nodes và kết thúc bằng một quyết định của các lá.

Trước khi tìm hiểu thêm về Decision Tree, chúng ta hãy làm quen với một số thuật ngữ.

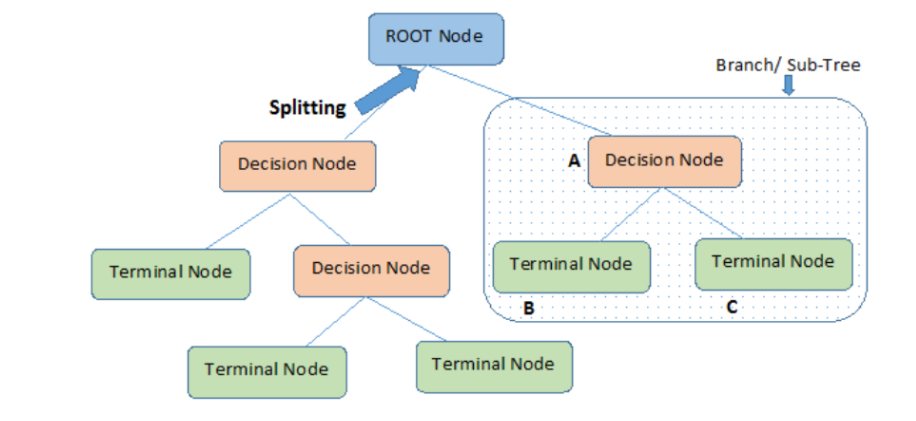
Root Nodes – Nó là nút hiện diện ở đầu Decision Tree từ nút này, quần thể bắt đầu phân chia theo các đặc điểm khác nhau.

Các Decision Nodes – các nút chúng ta nhận được sau khi tách các Root Nodes được gọi là Decision Nodes

Leaf Nodes – các nút không thể tách thêm được gọi là Leaf Nodes hoặc nút đầu cuối

Sub-tree – giống như một phần nhỏ của đồ thị được gọi là đồ thị con, tương tự như vậy một phần con của Decision Tree này được gọi là Sub-tree.

Pruning – không có gì khác ngoài việc cắt giảm một số nút để ngừng trang bị quá mức.

Các ứng dụng của cây quyết định là gì?

Cây quyết định được sử dụng để xử lý các tập dữ liệu phi tuyến tính một cách hiệu quả. Công cụ cây quyết định được sử dụng trong cuộc sống thực trong nhiều lĩnh vực, chẳng hạn như kỹ thuật, quy hoạch dân dụng, luật và kinh doanh. Cây quyết định có thể được chia thành hai loại; cây quyết định biến phân loại và biến liên tục.

Hãy hiểu Decision Tree với sự trợ giúp của ví dụ.

Ví dụ Decision Tree

Decision Tree lộn ngược có nghĩa là gốc ở trên cùng và sau đó gốc này được chia thành nhiều nút khác nhau. Decision Tree không là gì ngoài một loạt các câu lệnh if-else theo thuật ngữ của giáo dân. Nó kiểm tra xem điều kiện có đúng không và nếu đúng thì nó sẽ chuyển đến nút tiếp theo được đính kèm với quyết định đó.

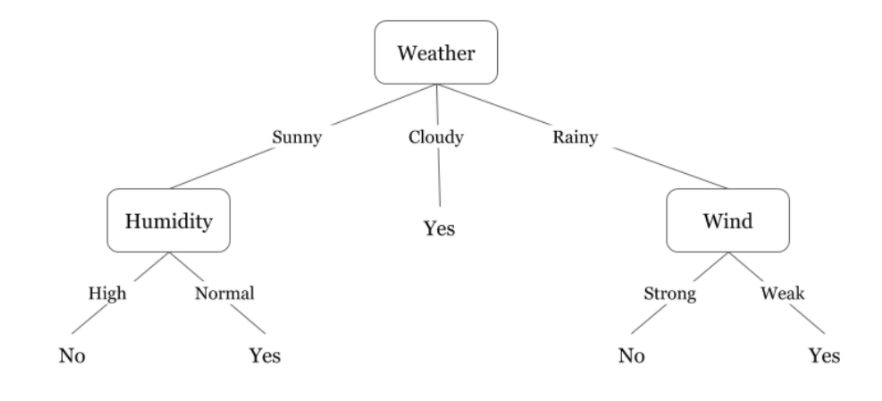
Trong sơ đồ dưới đây, đầu tiên cây sẽ hỏi thời tiết là gì? Trời nắng, mây, hay mưa? Nếu có thì sẽ chuyển sang tính năng tiếp theo là độ ẩm và gió. Nó sẽ kiểm tra lại xem có gió mạnh hay yếu, nếu gió yếu và trời mưa thì người đó có thể đi chơi.

Bạn có nhận thấy điều gì trong sơ đồ trên không? Chúng tôi thấy rằng nếu thời tiết nhiều mây thì chúng tôi phải đi chơi. Tại sao nó không tách ra nhiều hơn? Tại sao nó dừng lại ở đó?

Để trả lời câu hỏi này, chúng ta cần biết thêm một số khái niệm như entropy, information gain và Gini index. Nhưng nói một cách dễ hiểu, tôi có thể nói ở đây rằng kết quả đầu ra cho tập dữ liệu đào tạo luôn là có đối với thời tiết nhiều mây, vì không có sự lộn xộn ở đây, chúng tôi không cần phải chia nút thêm nữa.

Mục tiêu của Machine learning là giảm sự không chắc chắn hoặc rối loạn từ tập dữ liệu và để làm được điều này, chúng tôi sử dụng Decision Tree.

Bây giờ bạn phải nghĩ làm thế nào để tôi biết những gì nên là Root Nodes? Decision Nodes nên là gì? khi nào tôi nên ngừng chia nhỏ? Để quyết định điều này, có một số liệu được gọi là “Entropy”, là lượng không chắc chắn trong tập dữ liệu.

Thuật toán cây quyết định

Cây quyết định hay Decision Tree là một thuật toán đơn giản. Thuật toán này nhằm mục tiêu xây dựng các quy tắc hay luật lệ quyết định dựa theo cấu trúc cây với mỗi bộ luật tương ứng với nhánh lá của cây. Dữ liệu đầu vào có thể là dữ liệu missing không cần qua quá trình chuẩn hóa và tạo biến giả

Entropy

Entropy không là gì khác ngoài sự không chắc chắn trong tập dữ liệu hoặc thước đo sự rối loạn của chúng tôi. Hãy để tôi cố gắng giải thích điều này với sự trợ giúp của một ví dụ.

Giả sử bạn có một nhóm bạn quyết định họ có thể xem bộ phim nào cùng nhau vào Chủ nhật. Có 2 sự lựa chọn cho phim, một là “Lucy” và thứ hai là “Titanic” và bây giờ mọi người phải đưa ra lựa chọn của mình. Sau khi mọi người đưa ra câu trả lời của họ, chúng tôi thấy rằng “Lucy” được 4 phiếu bầu và “Titanic” được 5 phiếu bầu. Bây giờ chúng ta xem bộ phim nào? Bây giờ không khó để chọn 1 phim vì lượt bình chọn cho cả hai phim đều ngang nhau.

Đây chính xác là những gì chúng tôi gọi là rối loạn, có một số phiếu bầu bằng nhau cho cả hai bộ phim và chúng tôi thực sự không thể quyết định bộ phim nào chúng tôi nên xem. Sẽ dễ dàng hơn nhiều nếu số phiếu bầu cho “Lucy” là 8 và cho “Titanic” là 2. Ở đây chúng ta có thể dễ dàng nói rằng đa số phiếu bầu dành cho “Lucy” do đó mọi người sẽ xem bộ phim này.

Trong Decision Tree, đầu ra chủ yếu là “có” hoặc “không”

Công thức cho Entropy được hiển thị bên dưới:

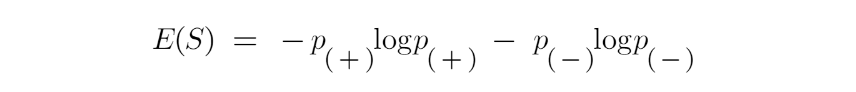
• Ở đây p + là xác suất của lớp dương
• p– là xác suất của lớp phủ định

S là tập con của ví dụ huấn luyện

Làm thế nào để Decision Tree sử dụng Entropy?

Bây giờ chúng ta biết entropy là gì và công thức của nó là gì, Tiếp theo, chúng ta cần biết rằng nó hoạt động chính xác như thế nào trong thuật toán này.

Về cơ bản, Entropy đo độ tạp chất của một nút. Tạp chất là mức độ ngẫu nhiên; nó cho biết dữ liệu của chúng ta ngẫu nhiên như thế nào. Một phân tách con thuần túy có nghĩa là bạn sẽ nhận được “có” hoặc bạn sẽ nhận được “không”.

Giả sử ban đầu một đối tượng có 8 “có” và 4 “không”, sau lần phân chia đầu tiên, nút bên trái nhận được 5 ‘y

es ’và 2″ no “trong khi nút bên phải nhận được 3” yes “và 2” no “.

Chúng ta thấy ở đây sự phân chia không trong sáng, tại sao vậy? Bởi vì chúng ta vẫn có thể thấy một số lớp phủ định trong cả hai nút. Để tạo một Decision Tree, chúng ta cần tính tạp chất của mỗi lần tách, và khi độ tinh khiết là 100%, chúng ta làm cho nó như một Leaf Nodes.

Để kiểm tra tạp chất của đặc điểm 2 và đặc điểm 3, chúng tôi sẽ thực hiện trợ giúp cho công thức Entropy.

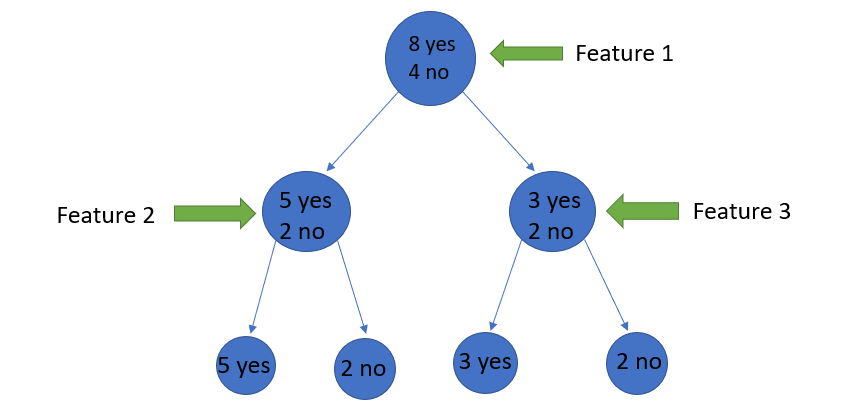
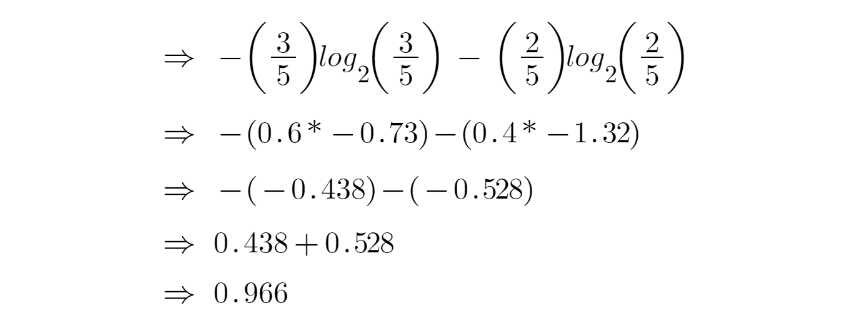
Chúng ta có thể thấy rõ ràng từ bản thân cây rằng nút bên trái có entropy thấp hoặc độ tinh khiết hơn nút bên phải vì nút bên trái có số lượng “có” nhiều hơn và rất dễ dàng để quyết định ở đây.

Luôn nhớ rằng Entropy càng cao thì độ tinh khiết càng thấp và tạp chất càng cao.

Như đã đề cập trước đó, mục tiêu của Machine learning là giảm độ không chắc chắn hoặc tạp chất trong tập dữ liệu, ở đây bằng cách sử dụng entropy, chúng ta đang nhận được tạp chất của một nút cụ thể, chúng ta không biết là entropy cha hay entropy của một nút cụ thể có giảm hay không.

Đối với điều này, chúng tôi mang đến một số liệu mới có tên là “Mức tăng thông tin” cho chúng tôi biết entropy mẹ đã giảm bao nhiêu sau khi tách nó bằng một số tính năng.

Information Gain

Information Gain đo lường việc giảm độ không đảm bảo do một số đặc điểm và nó cũng là yếu tố quyết định thuộc tính nào nên được chọn làm Decision Nodes hoặc Root Nodes.

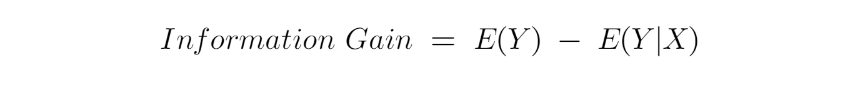
Nó chỉ là entropy của tập dữ liệu đầy đủ – entropy của tập dữ liệu được cung cấp một số tính năng.

Để hiểu rõ hơn điều này, chúng ta hãy xem xét một ví dụ:

Giả sử toàn bộ dân số của chúng ta có tổng cộng 30 trường hợp. Bộ dữ liệu là để dự đoán liệu người đó có đi đến phòng tập thể dục hay không. Giả sử 16 người đến phòng tập thể dục và 14 người không đi

Bây giờ chúng ta có hai tính năng để dự đoán liệu anh ấy / cô ấy có đi đến phòng tập thể dục hay không.

Xét thuộc tính là “Energy” nhận hai giá trị “high” và “low”

Thuộc tính 2 là “Motivation” có 3 giá trị “No motivation”, “Neutral” và “Highly motivated”.

Hãy xem Decision Tree của chúng ta sẽ được thực hiện như thế nào khi sử dụng 2 tính năng này. Chúng tôi sẽ sử dụng thu thập thông tin để quyết định tính năng nào nên là Root Nodes và tính năng nào sẽ được đặt sau khi tách.

Hãy tính toán entropy:

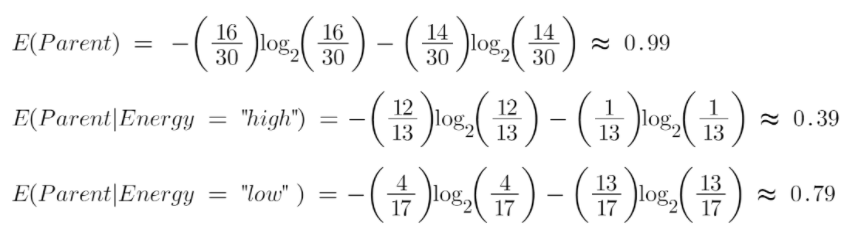
Để xem trung bình có trọng số của entropy của mỗi nút, chúng ta sẽ làm như sau:

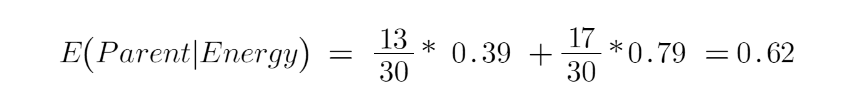
Bây giờ chúng ta có giá trị của E (Parent) và E (Parent | Energy), Information Gain sẽ là:

Entropy parent của chúng tôi là gần 0,99 và sau khi xem xét giá trị thu được thông tin này, chúng ta có thể nói rằng entropy của tập dữ liệu sẽ giảm 0,37 nếu chúng ta đặt “energy” làm Root Nodes.

Tương tự, chúng tôi sẽ thực hiện điều này với tính năng khác “Motivation” và tính toán mức tăng thông tin của nó.

Hãy tính toán entropy ở đây:

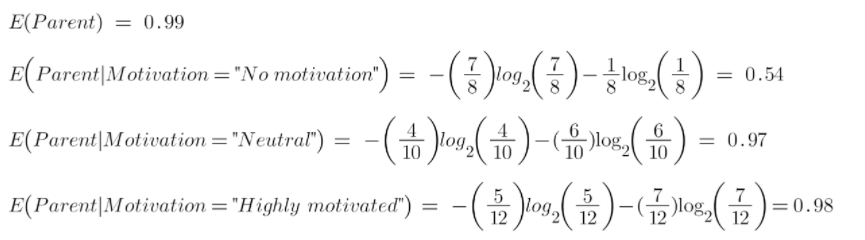
Để xem trung bình có trọng số của entropy của mỗi nút, chúng ta sẽ làm như sau:

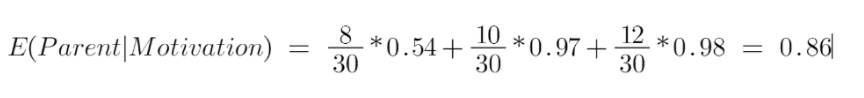
Bây giờ chúng ta có giá trị của E (Parent) và E (Parent | Motivation), Information Gain sẽ là:

Bây giờ chúng tôi thấy rằng tính năng “energy” giảm nhiều hơn, là 0,37 so với tính năng “Motivation”. Do đó, chúng tôi sẽ chọn đối tượng địa lý có mức tăng thông tin cao nhất và sau đó tách nút dựa trên đối tượng địa lý đó.

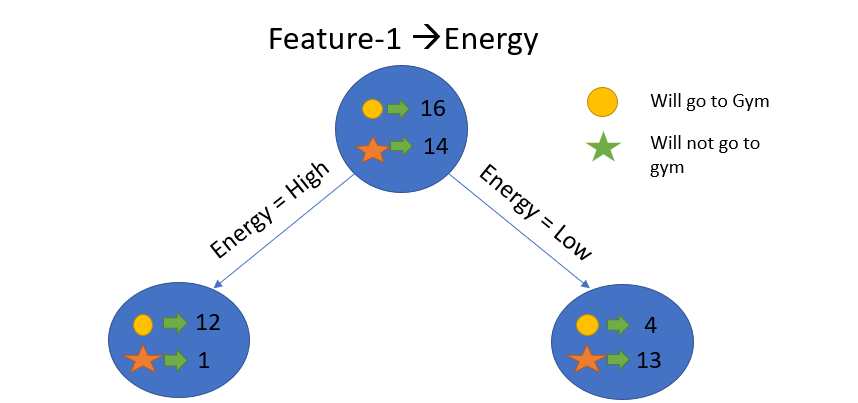
Trong ví dụ này, “energy” sẽ là Root Nodes của chúng ta và chúng ta sẽ làm tương tự đối với các nút phụ. Ở đây chúng ta có thể thấy rằng khi energy “cao” thì entropy thấp và do đó chúng ta có thể nói một người chắc chắn sẽ đến phòng tập thể dục nếu anh ta có energy cao, nhưng nếu energy thấp thì sao? Một lần nữa chúng tôi sẽ chia nút dựa trên tính năng mới là “Motivation”.

Khi nào thì ngừng chia nhỏ?

Chắc hẳn bạn đang tự hỏi mình câu hỏi này rằng khi nào thì chúng ta ngừng phát triển cây của mình? Thông thường, các bộ dữ liệu trong thế giới thực có một số lượng lớn các tính năng, điều này sẽ dẫn đến một số lượng lớn các phân tách, do đó tạo ra một cây khổng lồ. Những cây như vậy cần nhiều thời gian để xây dựng và có thể dẫn đến tình trạng quá sung. Điều đó có nghĩa là cây sẽ cho độ chính xác rất tốt trên tập dữ liệu huấn luyện nhưng sẽ cho độ chính xác kém trong dữ liệu thử nghiệm.

Có nhiều cách để giải quyết vấn đề này thông qua điều chỉnh siêu tham số. Chúng ta có thể đặt độ sâu tối đa cho Decision Tree của mình bằng cách sử dụng tham số max_depth. Giá trị của max_depth càng nhiều thì cây của bạn càng phức tạp. Lỗi đào tạo sẽ giảm đi nếu chúng ta tăng giá trị max_depth nhưng khi dữ liệu thử nghiệm của chúng ta hiển thị trên hình ảnh, chúng ta sẽ nhận được độ chính xác rất kém. Do đó, bạn cần một giá trị sẽ không trang bị quá mức cũng như không trang bị đầy đủ cho dữ liệu của chúng tôi và đối với điều này, bạn có thể sử dụng GridSearchCV.

Một cách khác là đặt số lượng mẫu tối thiểu cho mỗi lần đổ. Nó được ký hiệu là min_samples_split. Ở đây chúng tôi chỉ định số lượng mẫu tối thiểu cần thiết để thực hiện đổ. Ví dụ: chúng tôi có thể sử dụng tối thiểu 10 mẫu để đi đến quyết định. Điều đó có nghĩa là nếu một nút có ít hơn 10 mẫu

sau đó sử dụng tham số này, chúng ta có thể dừng việc chia nhỏ thêm nút này và biến nó thành một Leaf Nodes.

Có nhiều siêu tham số hơn như:

• min_samples_leaf – đại diện cho số lượng mẫu tối thiểu cần thiết để có trong Leaf Nodes. Bạn càng tăng số lượng, càng có nhiều khả năng trang bị quá mức.
• max_features – nó giúp chúng tôi quyết định số lượng tính năng cần xem xét khi tìm kiếm sự phân tách tốt nhất.

Pruning

Đó là một phương pháp khác có thể giúp chúng ta tránh overfitting. Nó giúp cải thiện hiệu suất của cây bằng cách cắt các nút hoặc nút con không quan trọng. Nó loại bỏ các nhánh có tầm quan trọng rất thấp.

Chủ yếu có 2 cách để Pruning:

• Pre-pruning – chúng ta có thể ngừng phát triển cây sớm hơn, có nghĩa là chúng ta có thể tỉa / loại bỏ / cắt một nút nếu nó có tầm quan trọng thấp trong khi phát triển cây.
• Post-pruning – khi cây của chúng ta đã được xây dựng đến độ sâu của nó, chúng ta có thể bắt đầu tỉa các nút dựa trên ý nghĩa của chúng.

Bài trước tôi đã giới thiệu về RL và bây giờ tôi sẽ nói về phương pháp đơn giản để chúng ta dễ dàng tiếp cập với RL.

Q-learning là gì?

Q-learning là một thuật toán học tăng cường không có mô hình (Model-free). Nó học tập dựa trên các giá trị (values-based). Các thuật toán dựa trên giá trị cập nhật hàm giá trị dựa trên một phương trình (đặc biệt là phương trình Bellman). Trong khi loại còn lại, dựa trên chính sách (policy-based) ước tính hàm giá trị với một chính sách tham lam có được từ lần cải tiến chính sách cuối cùng.

Q-learning is an off-policy learner 

Có nghĩa là nó học được giá trị của chính sách (policy) tối ưu một cách độc lập với các hành động của chủ thể (agent). Mặt khác, on-policy learner tìm hiểu giá trị của chính sách đang được thực hiện bởi chủ thể, bao gồm các bước thăm dò và họ sẽ tìm ra một chính sách tối ưu, có tính đến việc khám phá (exploration) vốn có trong chính sách.

"Q" ở đây là gì?

Chữ ‘Q’ trong Q-learning là viết tắt của "quality" chất lượng. Chất lượng ở đây thể hiện mức độ hữu ích của một hành động (action) nhất định trong việc đạt được một số phần thưởng (reward) trong tương lai.

Yếu tố chính của Q-learning

• Q*(s, a) là giá trị kỳ vọng (phần thưởng chiết khấu tích lũy) của việc thực hiện hành động (action) a ở trạng thái (state) s và sau đó tuân theo chính sách tối ưu (optimal policy).
• Q-learning sử dụng "Sự khác biệt theo thời gian" Temporal Differences (TD) để ước tính giá trị của Q*(s, a). TD là một chủ thể (agent) có khả năng học hỏi từ môi trường thông qua các giai đoạn (episodes) mà không có kiến ​​thức trước về môi trường.
• Chủ thể (agent) duy trì một bảng Q[S, A], trong đó S là tập các trạng thái và A là tập các hành động.
• Q[s, s] đại diện cho ước tính hiện tại của nó là Q*(s, a).

Reinforcement Learning là gì?

Fig. 1. An agent interacts with the environment, trying to take smart actions to maximize cumulative rewards.

Giả sử, chúng tôi có một đại lý trong một môi trường không xác định và đại lý này có thể nhận được một số phần thưởng bằng cách tương tác với môi trường. Người đại diện phải thực hiện các hành động để tối đa hóa phần thưởng tích lũy. Trong thực tế, kịch bản có thể là một bot chơi trò chơi để đạt được điểm số cao, hoặc một robot cố gắng hoàn thành các nhiệm vụ vật lý với các vật phẩm vật lý; và không chỉ giới hạn ở những thứ này.

Bạn đã bao giờ trách móc hoặc đánh đập con chó của mình một cách nghiêm khắc vì những hành động sai trái sau khi nó làm chưa? Hay bạn đã bao giờ huấn luyện một con vật cưng và thưởng nó cho mỗi lệnh đúng mà bạn yêu cầu chưa? Nếu bạn là chủ sở hữu vật nuôi, có lẽ câu trả lời của bạn sẽ là ‘Có’. Bạn có thể nhận thấy một khi bạn làm như vậy thường xuyên từ khi nó còn nhỏ, những việc làm sai trái của nó giảm dần từng ngày. Và cũng giống như nó sẽ học hỏi từ những sai lầm và rèn luyện bản thân thật tốt.

Là con người, chúng ta cũng đã từng trải qua điều tương tự. Bạn có nhớ không, ở trường tiểu học của chúng tôi, các giáo viên của trường chúng tôi đã thưởng cho chúng tôi những ngôi sao khi chúng tôi đã hoàn thành tốt các công việc của trường. Đây chính xác là những gì đang xảy ra trong "Học tăng cường" (RL).

Reinforcement Learning is one of the most beautiful branches in Artificial Intelligence

Mục tiêu của RL là tìm kiếm một chiến lược tốt cho "chủ thể" từ các "trải nghiệm" và nhận được phản hồi từ những tương tác với môi trường. Với chiến lược tối ưu, chủ thể có khả năng chủ động thích ứng với môi trường để tối đa hóa phần thưởng trong tương lai.

Các khái niệm chính trong RL

Chủ thể (agent) đang hoạt động trong môi trường (environment). Cách môi trường phản ứng với các hành động nhất định được xác định bởi một mô hình (model) mà chúng ta có thể biết hoặc có thể không biết. Chủ thể (agent) là người đưa ra quyết định (make a decision), có thể ở một trong nhiều trạng thái (states) (s ∈ S) của môi trường, và chọn thực hiện một trong nhiều hành động (actions) (a ∈ A) để chuyển từ trạng thái này sang trạng thái khác. Trạng thái nào mà chủ thể sẽ có được quyết định bởi xác suất (probabilities) chuyển đổi giữa các trạng thái (P). Khi một hành động được thực hiện, môi trường mang lại phần thưởng (reward) (r ∈ R) dưới dạng phản hồi.

RL là khoa học về việc đưa ra các quyết định tối ưu bằng cách sử dụng kinh nghiệm. Chi tiết hơn, quá trình RL bao gồm các bước đơn giản sau:

Mô hình hóa toán học của RL

1. Đây là một ví dụ trực quan về Agent:

2. Enviroment xung quang của Agent, nơi mà agent tồn tại và tương tác:

3. Dựa trên State S(t) của enviroment hiện tại mà agent sẽ đưa ra action a(t):

4. Sau khi nhận được sự tương tác từ agent thì enviroment có sự chuyển đổi trạng thái đối với agent:

5. State lúc này của enviroment là S(t+1), tức ở thời điểm t+1:

6. Lúc này, agent nhận được reward r(t). Reward này phụ thuộc vào action a(t) của agent và State S(t) của enviroment ở thời điểm trước đó, tức là ở thời điểm t:

7. Vì ta không biết thời điểm kết thúc của sự lặp đi lặp lại này nên tổng reward sẽ là một chuỗi vô hạn của các reward thành phần tại các thời điểm khác nhau kể từ thời điểm t (lúc đầu):

8. Chúng ta có thể khai triển chuỗi vô hạn này như sau:

9. Vì chuỗi này không thể nào hội tụ (convergence) được nên trên thực tế các nhà nghiên cứu có thể dùng một cái trick để chuỗi này có thể hội tụ được. Như hình dưới đây, họ đưa vào thêm một term thường được gọi là discount factor (discount rate) để làm cho chuỗi này hội tụ. 

Lưu ý việc hội tụ là bắt buộc nếu bạn muốn train thành công một agent nói riêng hay một mạng Neural Network nào đó nói chung.

Tất cả những thứ trên nó dựa trên một framework được gọi là Markov Decision Processes (MDPs). Về cơ bản thì một MDP cung cấp một framework toán học cho việc modelling các tình huống decision-making. Ở đây, các kết quả (outcomes) xảy ra một cách ngẫu nhiên một phần và phần còn lại thì phụ thuộc trên các action của agent (hoặc decision maker) đã tạo ra trước đó. reward thu được bởi decision maker phụ thuộc trên action mà decision maker chọn và dựa trên cả hai State mới (S(t+1)) và cũ (S(t)) của enviroment.

Để có thể train được agent thì mục tiêu của chúng ta là phải tìm được policy $\pi$$\pi$ sao cho:
* $\beta$ là discount factor và $\beta$ < 1

Về cơ bản thì chúng ta đang cố gắng để maximize tổng của tất cả các reward (có tính đến discount factor như đã đề cập ở trên) ở mỗi state cụ thể từ lúc bắt đầu đến khi kết thúc (dẫu cho T tiến về vô cùng, vì chúng ta chưa biết khi nào thì quá trình này kết thúc nên nó vẫn luôn là một chuỗi vô hạn), và đương nhiên là phải dựa trên policy $\pi$ vì agent của chúng ta base trên nó để chọn reward tốt nhất mà. Bản chất thì đây là một bài toán tối ưu (optimazation problem).

Ở trên là một tiêu chí mà chúng ta có thể dùng để optimize cho việc tìm ra nghiệm (optimal policy). Cụ thể chúng ta gọi tiêu chí này là infinite horizon sum reward criteria. Phụ thuộc vào các criteria khác nhau mà chúng ta sẽ có các algorithm khác nhau để tìm ra optimal policy. Với infinite horizon sum reward criteria thì chúng ta có thể sử dụng một thuật toán RL cũng khá kinh điển đó là Q-Learning để giải quyết, tôi sẽ giới thiệu trong bài viết tiếp theo.

Phân loại các phương án trên RL

Để phân loại rõ ràng các thuật toán trên RL khá phức tạp, chúng ta có thể nhìn hình bên dưới và tạm thời chia theo vài trường hợp chính: 

Fig. 2. Summary of approaches in RL based on whether we want to model the value, policy, or the environment. (Image source: reproduced from David Silver’s RL course lecture 1.)

• Model-free: thuật toán ước tính chính sách tối ưu mà không cần sử dụng hoặc ước tính động lực học (chức năng chuyển đổi và phần thưởng) của môi trường. 

• Model-based là một thuật toán sử dụng hàm chuyển tiếp (và hàm phần thưởng) để ước tính chính sách tối ưu.

• On-policy: Sử dụng kết quả xác định hoặc mẫu từ chính sách mục tiêu (target policy) để đào tạo (train) thuật toán.

• Off-policy: Đào tạo về cách phân phối các chuyển đổi (transitions) hoặc các tập (episodes) được tạo ra bởi một chính sách (policy) hành vi khác chứ không phải do chính sách mục tiêu tạo ra.

Ngoài ra, nếu nhìn tổng quát hơn ta có thể phân loại Rl thành những nhóm như hình bên dưới

Tiếp theo, để tạo nền tảng kiến thức vững vàng trước khi đi vào phân tích cũng như phát triển thuật toán trên RL các bạn nên tìm đọc và hiểu về cách khái niệm như Trasition, Reward, Policy, Value Function,... đặc biệt là Markov Decision Processes và Bellman Equations (có thời gian mình sẽ phân tích thêm về phần này) từ sách. 

Ví dụ

Reinforcement Learning: An introduction (link) 

Hoặc tổng hợp khác của tôi ở đây

P/s: từ tài liệu tiếng anh có nhiều từ rất khó để dịch sát nghĩa sang tiếng việt nên khó tránh khỏi sai sót, nhưng vì mong muốn các bạn ở VN có nhiều nguồn tài liệu để tiếp cận hơn. Các bạn có khả năng đọc hiểu tiếng anh thì nên đọc sách góc sẽ tốt hơn. Các phần tiếp theo mình đã xử lý dưới xong rồi, mình có thời gian sẽ tiếp tục, kết hợp với code mô phỏng. Hy vọng các bạn tìm thấy được sự thú vị từ đây! have fun 😏